
Description:
Situations Matter – Understanding the Structure of Word Problems (Part 2)
In Part 2 of our problem-solving series, we dive into how to support students in grades 3–5 with multiplication and division word problems. We unpack the three key situation types—Equal Groups, Arrays, and Multiplicative Comparison—and explore how to set clear goals, provide scaffolds, and use conceptual models to help students reason through problems.
Rooted in the Standards of Mathematical Practice and Universal Design for Learning (UDL), this episode emphasizes how tools, language, and intentional planning can empower all learners. You’ll hear how these strategies build fluency, support reasoning, and help students make sense of math—not just memorize procedures.
Explore visuals and classroom tools at MathUniversallySpeaking.com, where you’ll also find links to the podcast on your favorite platforms.
#MathUniversallySpeaking | #UDLinMath | #InclusiveMathInstruction | #StandardsOfMathematicalPractice
Transcript
Situations Matter: Understanding the Structure of Word Problems (Part 2)
🎙️ Hey math friends! Welcome back to our humble podcast, Math Universally Speaking! Before we dive in, I want to remind you to head over to Math: Universally Speaking at MathUniversallySpeaking.com. You’ll find links to listen on your favorite podcast platforms—and helpful resources to support what we’re talking about today. This is Part 2 of a two-part series on problem solving. In Part 1, we explored what problem solving really is—and what it isn’t. We talked about moving beyond keywords and tricks to help students reason and make sense of problems. If you haven’t checked it out, go back and give it a listen.
In this episode, we’re digging into how to support our students in grades 3–5, especially when they’re working through multiplication and division word problems. We’ll focus on how setting clear goals, offering the right scaffolds, and choosing the best tools can truly help students become confident, capable problem solvers.
Let’s Start with Clear Goals:
According to the Focus Documents from Achieve the Core, the big ideas in grades 3–5 math are multiplication, division, and fractions—and developing them through conceptual understanding, procedural skill, and real-world problem solving. For today, we’re zooming in on problem solving with multiplication and division.
Students encounter three main situation types when solving multiplication and division word problems. I encourage you to check out the visual models on MathUniversallySpeaking.com while listening to this portion of the podcast:
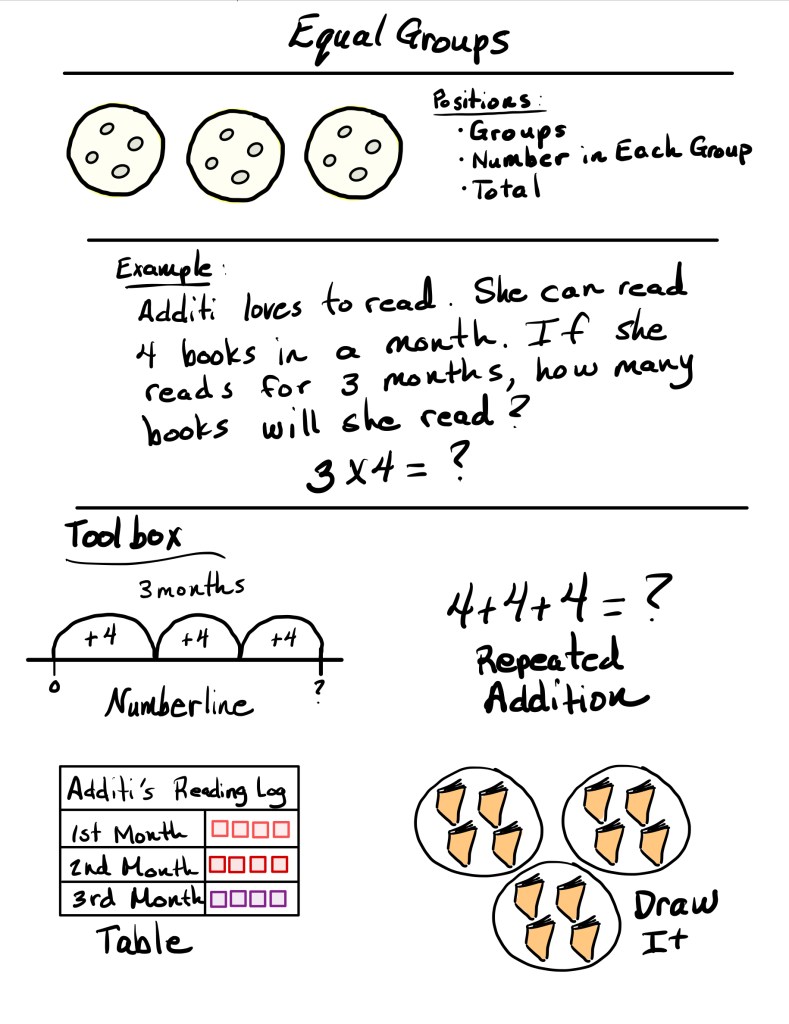
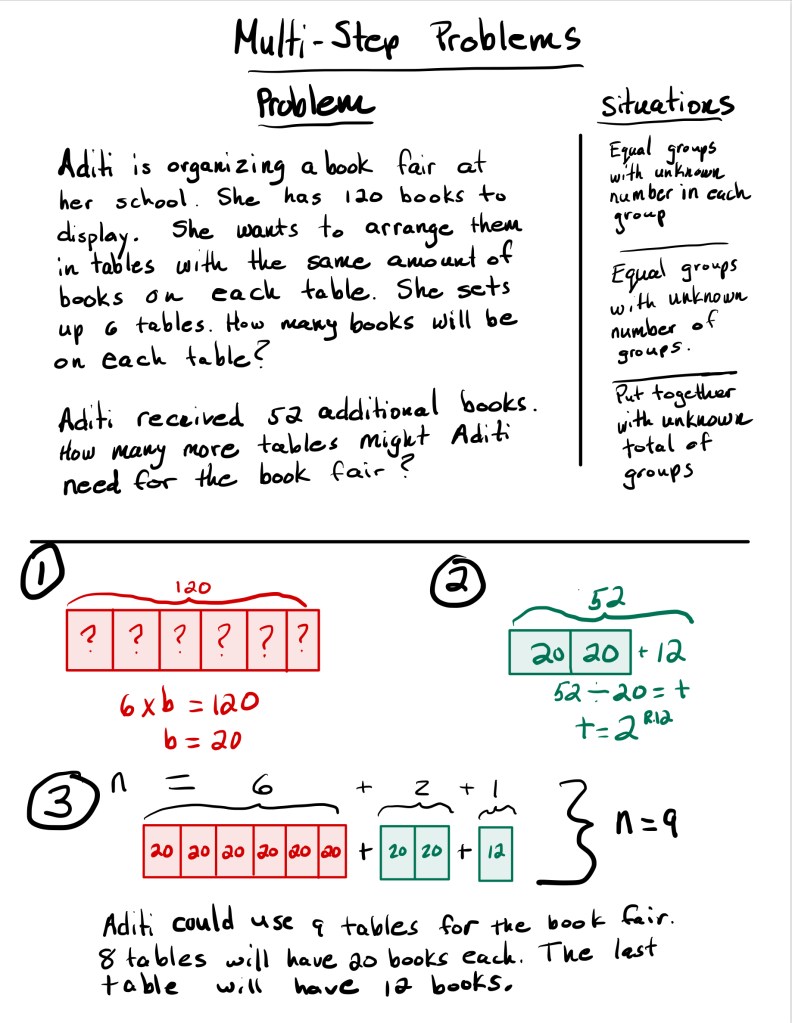
- Equal Groups – Students identify the number of groups, how many in each group, and the total. They often begin with fair-share thinking to ensure that each group has an equal amount. Over time, students shift from just finding totals to finding missing groups or missing quantities in each group. This is how students begin to show the connection between multiplication and division—as they work to find the unknown in any three positions in the problem.
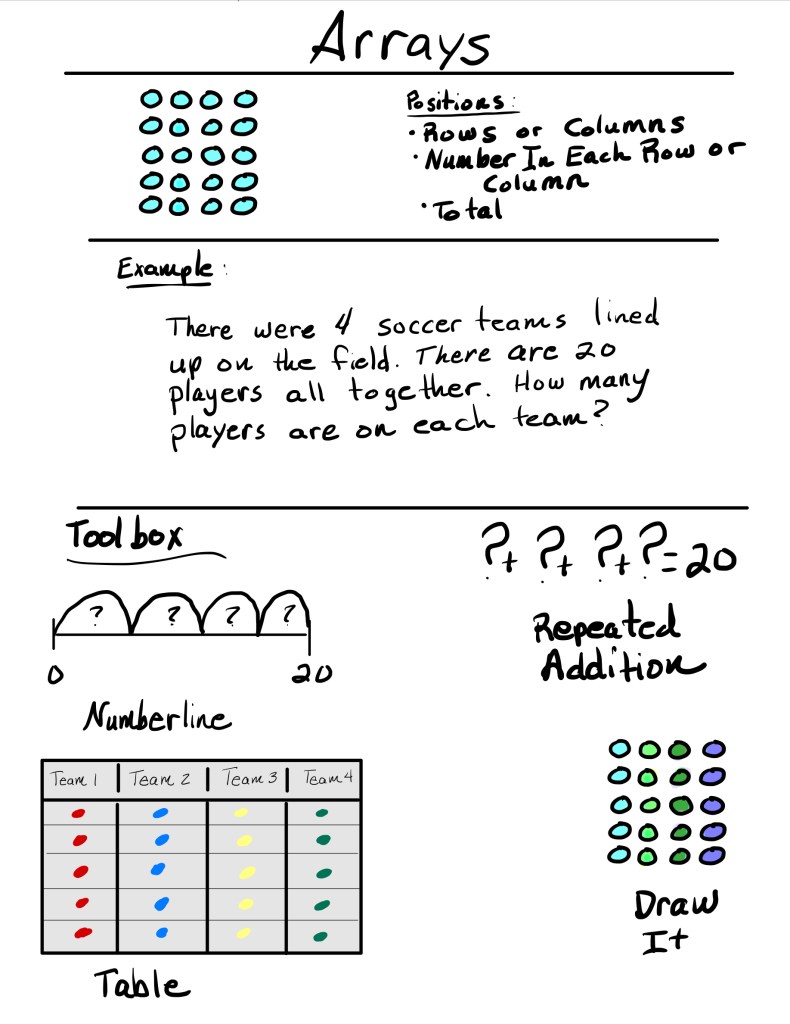
- Arrays – Students work through the relationships between rows or columns, the quantities in each row or column, and the total. Unknowns can appear in any of these positions. Sometimes, students fall back on “equal groups” thinking to solve array problems—and that’s okay. They are similar. It might be their entry point. However, it will be important to focus on the understanding of arrays when you discuss it in the context of the problem. Arrays are also foundational for understanding area and area models later on.
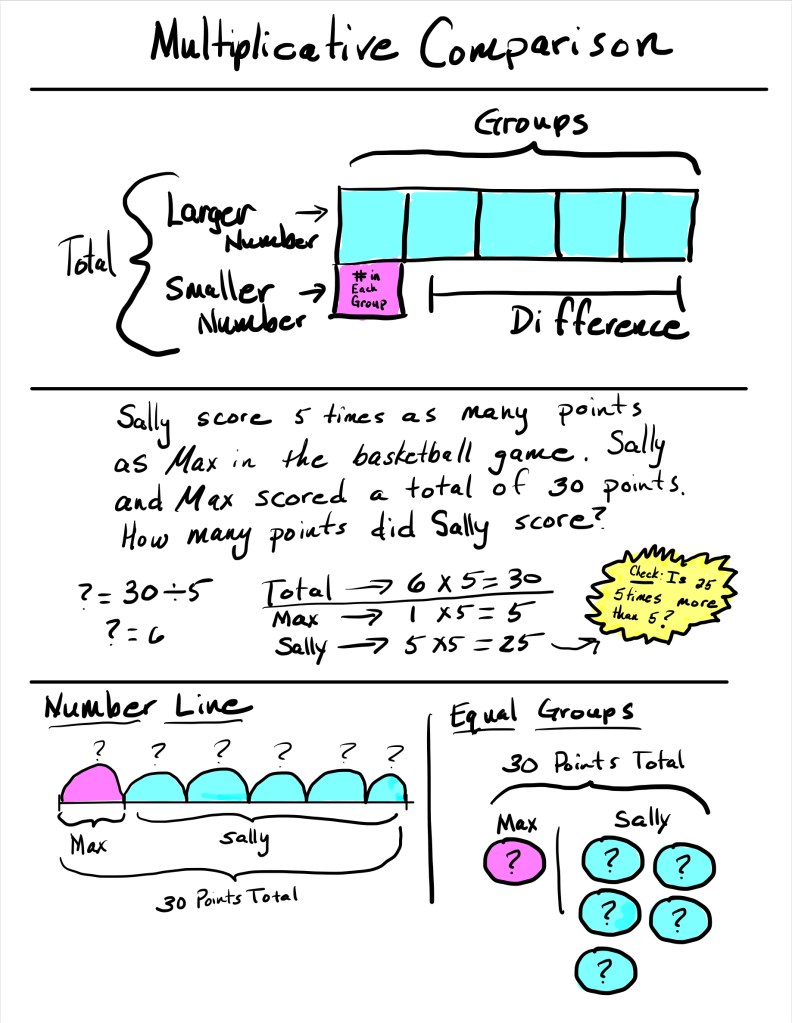
- Multiplicative Comparison – This shows up in 4th grade and is similar but different from the additive comparison they learned in earlier grades. Just like with additive comparisons, we can anchor the conversation with the larger number, smaller number, and difference—but now, it’s multiplicative. Instead of comparing “how many more,” students compare “how many times more.” The larger number is composed of groups, and the smaller number tells us how many are in each group. The unknown could be any of these parts—including the total of the larger and smaller numbers.
- This can definitely get complex. That’s why it’s so important to reduce confusion by using visual models and consistent language to describe the parts of the problem and helping students identify the unknown clearly.
As we said in part one, these problem types aren’t just about plugging in numbers or finding key words to identify operations. They help students build reasoning, and that’s the heart of real problem solving.
Fluency Comes with Support:
This ties directly into **UDL’s Consideration 5.3 (Building fluencies with graduated support for practice and performance. Sometimes we over-focus on whether students have their math facts memorized. But here’s the thing—students might still be learning their basic facts while tackling complex reasoning in problems. And that’s okay…for now!
If students aren’t able to automatically recall their math facts while working through a multi-step problem, it doesn’t mean they can’t solve problems. We can remove that barrier. Give them tools—like multiplication charts or calculators—so they can stay focused on the current goal: problem solving. These supports reduce cognitive load and help students stay engaged in deep thinking.
Tools Should Work for the Student:
Conceptual models are like blueprints. They help students map out a problem before jumping into equations. This is reflected in SMP #5 (Use appropriate tools strategically) and Universal Design for Learning Consideration 5.2 (Use multiple tools for construction, composition, and creativity).
We want students to move flexibly between models and equations. Pictures, bar models, number lines, arrays, and equal groups aren’t substitutes for equations or procedures—and vice versa. They help students reason abstractly and quantitatively, and accurately connect the models to the operations and quantities in the equation.
We’ve talked a lot about models as a way to make sense of the problem. But some students may start with an equation. Even if they get the correct answer, ask them to draw a model that shows why it worked. This helps them create a more viable argument (SMP #3).
And just like before—some students may need calculators or multiplication charts. That’s still okay if we’re digging into the thinking behind problem solving.
Keep the Main Thing the Main Thing:
If you’re a Philly sports fan like I am, you’ve probably heard our quarterback say, “Keep the main thing the main thing.”
In math instruction, that means clarity. What are we really assessing?
If we are using formative assessments or standardized assessments, we need to be tight on the learning goal. We want students to:
- Interpret the problem using the Situation Types
- Leverage the relationships between quantities
- Identify the unknowns
- Execute a solid strategy
- Work precisely to find an accurate solution
When we communicate these learning goals clearly, students are more likely to stay focused on those goals, build their capacity to show their thinking in multiple ways, and truly engage in problem solving.
🎙️ Thanks for joining me for Part 2 of our problem-solving series here on Math Universally Speaking. We’re building a community around strong, inclusive math practices—and your voice matters. So let’s keep the conversation going!
👉 Visit MathUniversallySpeaking.com where you’ll find links to this podcast on your favorite platforms and helpful resources to support our conversation. Don’t forget to share your takeaways using the hashtag #MathUniversallySpeaking.
Until next time—keep supporting your students to think deeply, work flexibly, and grow in confidently.
Other Resources
Problem Solving Standards
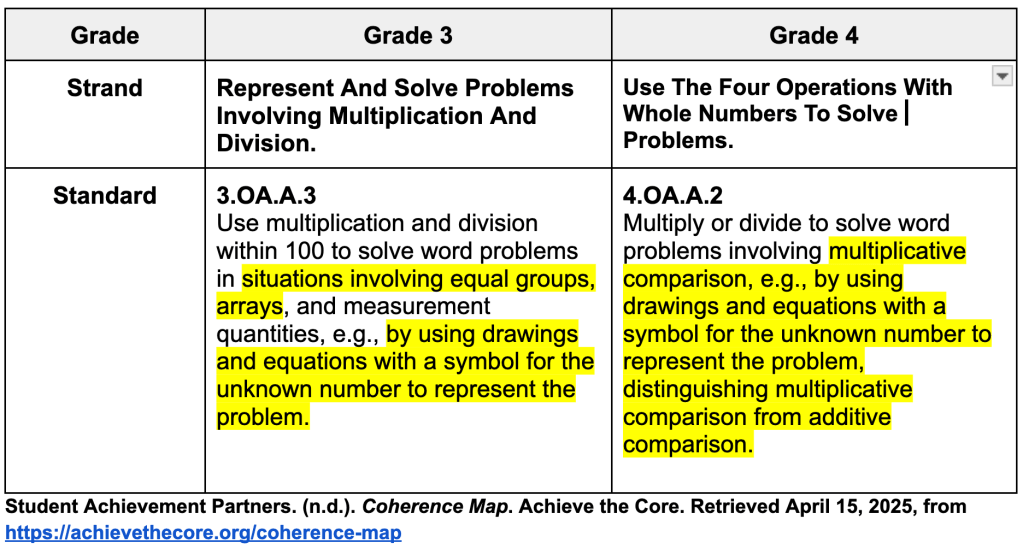
Anchor Chart Examples:
These anchor charts are loaded with information. You do not need to add this much to your anchor chart. These are just some suggestions on information you can use for Multiple Means of Representation.
💬 Professional Development Questions
- How do the three multiplication and division situation types—Equal Groups, Arrays, and Multiplicative Comparison—show up in your current curriculum materials?
- What opportunities do students have to make sense of these situations through reasoning, rather than relying on keywords or procedural tricks?
- How might you adjust your instruction or assessments to more clearly align with the learning goal of problem solving?
- Consider especially SMP #1 (Make sense of problems), SMP #2 (Reason abstractly and quantitatively), and SMP #5 (Use appropriate tools strategically).
- What supports (such as tools, scaffolds, or instructional routines) could you add or adjust to ensure all students—including those still building fluency—can access and engage in problem solving?
References:
Achieve the Core. (n.d.). Mathematics focus by grade level. Achieve the Core. Retrieved April 5, 2025, from https://achievethecore.org/category/774/mathematics-focus-by-grade-level
Achieve the Core. (n.d.). Situation types for operations in word problems. Achieve the Core. Retrieved April 5, 2025, from https://achievethecore.org/page/932/situation-types-for-operations-in-word-problems
CAST. (2018). Universal design for learning guidelines version 2.2. CAST. Retrieved April 5, 2025, from https://udlguidelines.cast.org/
National Governors Association Center for Best Practices, & Council of Chief State School Officers. (2010). Common Core State Standards. http://www.corestandards.org
OpenAI. (2024). ChatGPT (Mar 14 version) [Large language model]. https://chat.openai.com/
Rufo, J. M., & Martiello, R. (2024). Conquering math myths with universal design: An inclusive instructional approach for grades K–8. ASCD.



Leave a comment