
Description:
Situations Matter – Understanding the Structure of Word Problems (Part 1)
Welcome to Math Universally Speaking, the podcast where inclusive math instruction takes center stage. Hosted by educator and author Ron Martiello, each episode explores how Universal Design for Learning (UDL) can transform the way we teach and reach all learners.
In this episode, Situations Matter: Understanding the Structure of Word Problems, Ron breaks down the three foundational types of addition and subtraction word problems—Put Together/Take Apart, Add To/Take From, and Compare. Discover why understanding these structures early on sets the stage for success with more complex math later. Packed with practical tips and UDL-aligned strategies, this episode helps educators move beyond keywords and toward deeper, more flexible problem-solving.
Join us and reimagine what’s possible in math—one situation at a time.
Transcript
Situations Matter: Understanding the Structure of Word Problems
Welcome to Math Universally Speaking. I’m Ron Martiello, and today I want to chat with you about one of my absolute favorite strands of standards in math. These standards live in the K-2 space but have a huge impact on students in grades 3, 4, 5, and even 6 as they begin to tackle more complex word problems.
A couple episodes ago, I touched on the Standard of Marth Practice #1: Making sense of problems and persevering through them, and I briefly mentioned something called “situation types.” Well, today, we’re going deeper.
So for my friends in the upper grades, stick with me. Because what we teach in K-2 forms the bedrock of how your students will later make sense of the operations and structures of word problems. This work is foundational and should not be overlooked.
Let’s start by grounding ourselves in what the major work of grades K-2 is all about. According to the focus documents on Achievethecore.com, that major work includes:
- Addition and subtraction
- Understanding the structure of base-10
Sounds pretty straight forward. Right, however, there is a third part. Students are expected to learn those big ideas through a balanced approach including conceptual understanding, procedural skill and fluency, and application—especially in real-world problem solving.
Now within the domain of Operations & Algebraic Thinking lives a strand of standards that directly relate to word problems. And this is where my favorite work begins.
There are three situation types students learn to understand and solve with addition and subtraction:
- Put Together / Take Apart
- Add To / Take Away
- Compare
Each of these situations includes different structures and unknowns in different positions in the word problem. Let’s break them down.
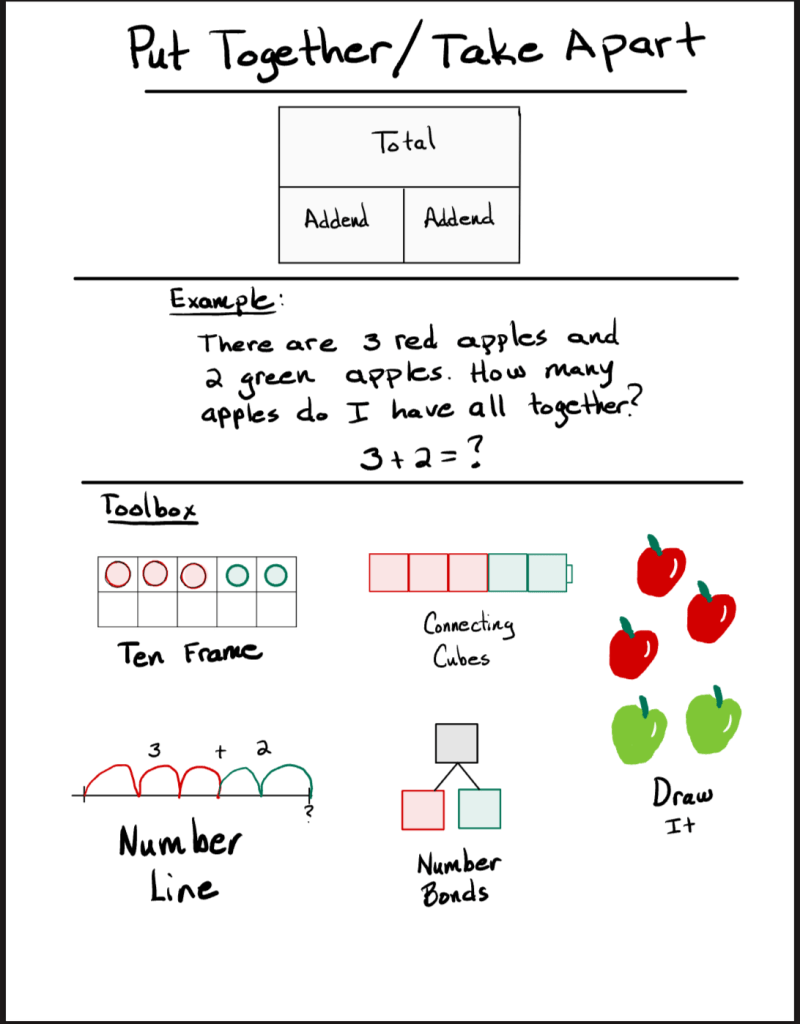
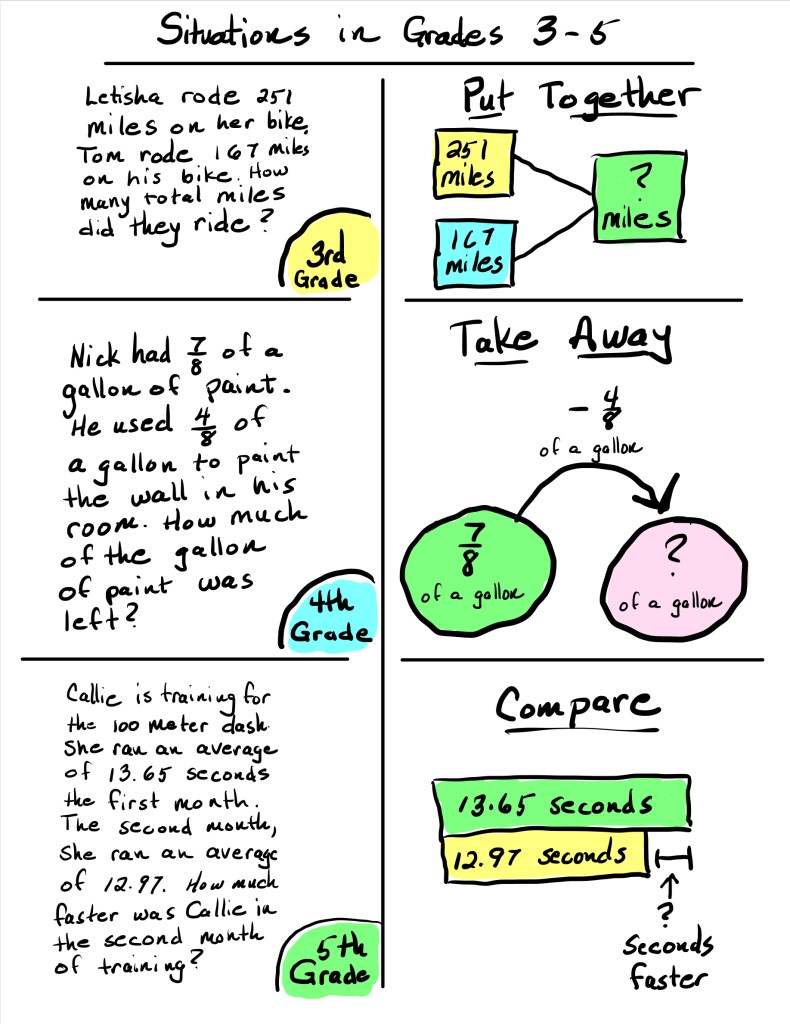
1. Put Together / Take Apart
This is often the first type of problem students encounter in kindergarten. They might not yet use the term “addends,” but what they are doing is combining two quantities to find a total. For example: I have three green apples and two red apples. How many apples do I have in all?
It seems simple, but it’s the starting point for building that foundational understanding of part-part-whole relationships.
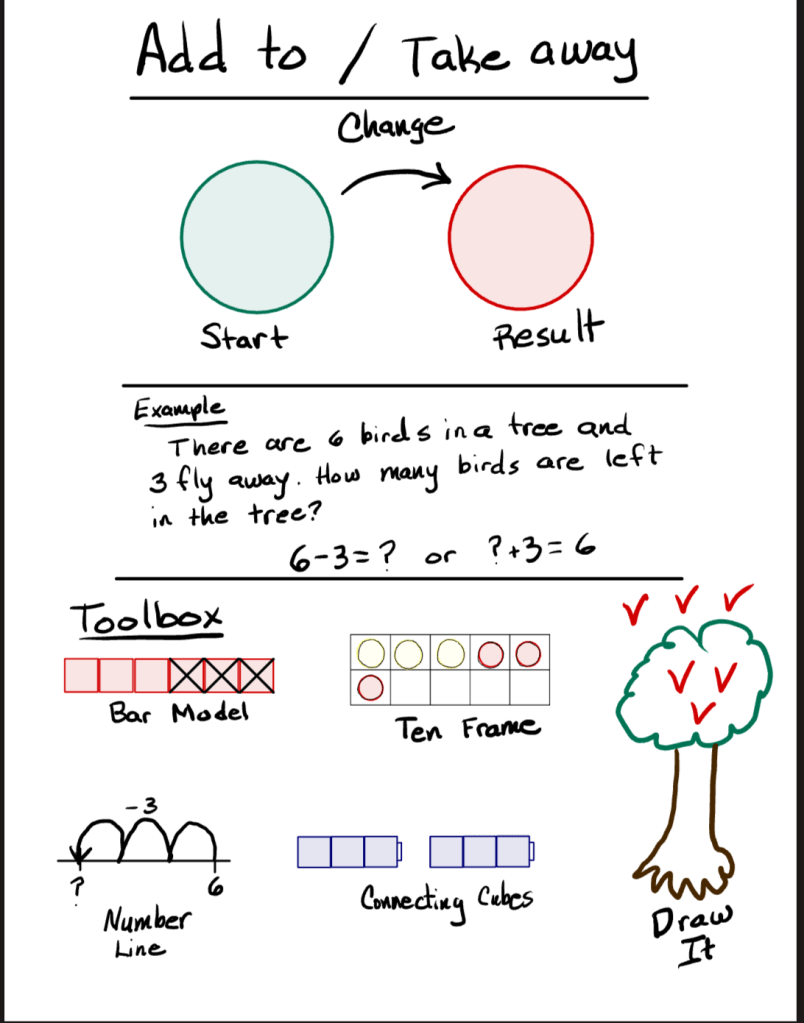
2. Add To / Take Away
Let’s use the classic word problem about birds in a tree, so we can illustrate this this situation. It goes something like this:
- There are 9 birds in a tree. 3 fly away. How many are left? (Take From)
- Or: There are 6 birds in a tree. 3 more fly in. How many now? (Add To)
No matter the context, adding players to a baseball team, or little brother eating the cookies you just baked, these problems help students grasp the concept of change—something being added or removed from a quantity.
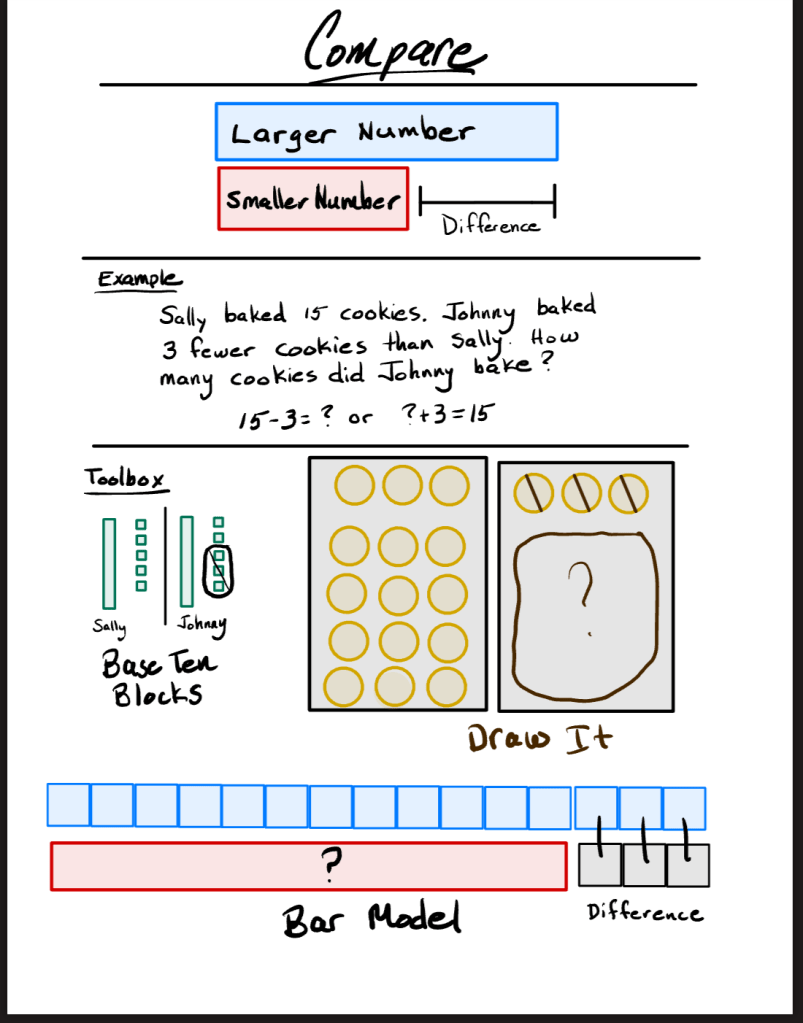
3. Compare
This word problem situation usually enters the scene in first grade. It involves analyzing how two quantities relate to one another:
- Sally has 7 stickers. Johnny has 4. How many more stickers does Sally have than Johnny?
Here, students are dealing with larger, smaller, and difference quantities. These problems get nuanced quickly, especially when the unknown is in any one of those positions.
Now, here’s where it really starts to matter.
Students often get tripped up because they try to match operations to keywords. You know the ones: “altogether” must mean add, but language isn’t always that neat. “Altogether” doesn’t guarantee an addition situation. And teaching students to chase keywords sets them up for confusion down the line.
Instead of focusing on trick words we should be helping students understand the relationships between quantities in the problem.
Let’s take a closer look:
- In Put Together / Take Apart, you have two addends and a total. What’s unknown? Are we looking for an addend or the total?
- In Add To / Take Away, you have a start number, a change number, and a result. Which is missing?
- In Compare, you have a larger quantity, a smaller quantity, and the difference. Which one are you solving for?
And in second grade, when students begin to solve two-step problems, they can actually stack these models to show their reasoning. For example, one part of the problem might involve a take away situation, and the next might require a comparison situation.
Here is the beauty of it: when we teach students to approach word problems by exploring the situations and the relationships between the quantities, students can use different tools to reason through problems. They may choose to represent the problem with connecting cubes, open number lines, or bar models. When using equations to represent the problem, a student may use addition or subtraction. For example, in a takeaway situation, where there is a missing start number, students may decide to show their understanding through an addition equation or a subtraction equation. In either case, they can use symbol to show where the unknown lies in the equation. Exercising reasoning becomes the goal not just finding the solution.
This is the heart of problem solving.
Supporting Students’ Understanding:
So how can we support students in building this understanding. Enter Universal Design for Learning and Multiple Means of Representation?
- Clarify vocabulary, symbols, and language structures through modeling: Provide visual models of these situations so students can see the structure. Think of it like a blueprint to understand what’s happening in the problem.
- Support decoding of text, mathematical notation, and symbols using Numberless Word Problems: When numbers become the barrier, temporarily remove the numbers so students can comprehend the problem and focus on the relationships between the quantities. Ask: What’s happening here? Is this a comparison? Are we taking something apart?
- Cultivate multiple ways of knowing and making meaning by giving the answer first: This is a great UDL-aligned strategy. Give students the result, then have them explore how the quantities could relate to arrive at that answer. It forces them to focus on relationships rather than rushing to calculate.
Let’s be real—sometimes I hear folks say, “This is too complex for kids.” However, I ask you to consider this… These are generalizations that help students navigate any word problem. And honestly, what could be more foundational than understanding the structure of how problems work?
If we don’t invest time in this thinking early on, we risk setting students up for struggle when they encounter more abstract problems with fractions, decimals, or multi-step reasoning with all four operations in upper elementary grades.
Remember—this work has coherence. It builds. And it matters.
In a future episode, we’ll take on the other three situation types found in multiplication and division. But for now, let’s make sure we’re giving students the time, language, and strategies they need to truly understand these foundational situations. For your convenience I have also posted some graphics on the website to support your understanding of the situation types as you design your future lessons.
Thanks for joining me on Math Universally Speaking. Don’t forget to follow the podcast and use #MathUniversallySpeaking to join the conversation on social media. Let’s reimagine math together—one situation at a time.
Other Resources
Problem Solving Standards
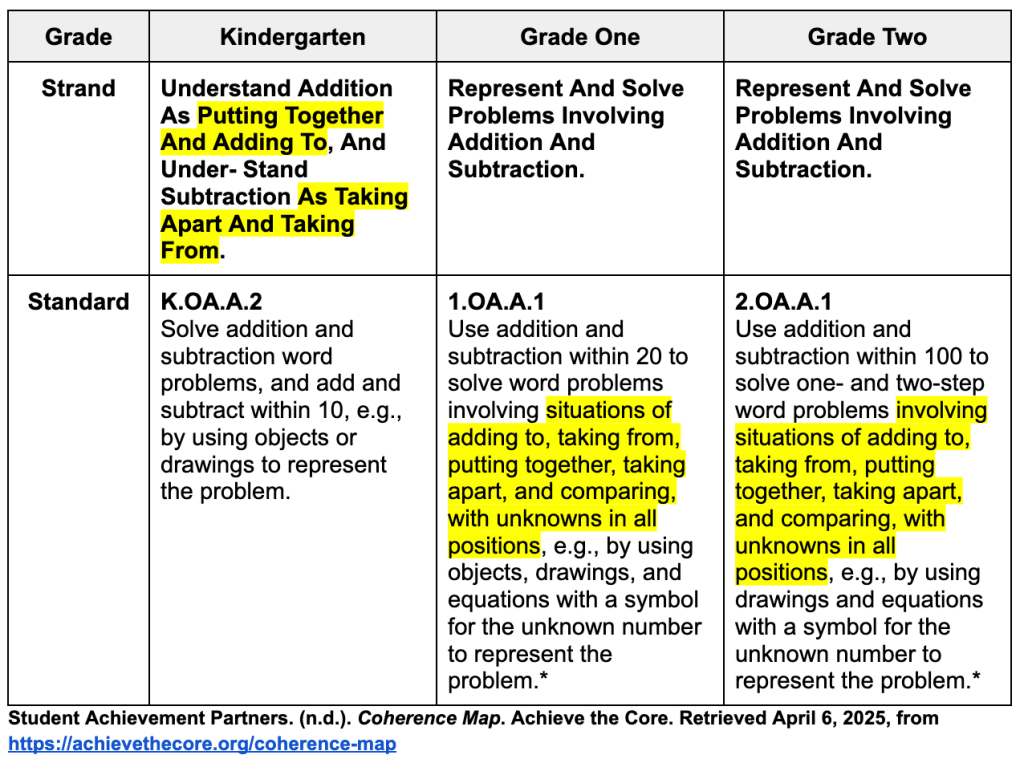
Anchor Chart Examples:
These anchor charts are loaded with information. You do not need to add this much to your anchor chart. These are just some suggestions on information you can use for Multiple Means of Representation.
*Note: I have used the phrase “Take Away” rather than “Take From”. I have had more success with this term. Please feel free to use the phrase that works best for you and your students.
Professional Development
- Which of the three primary word problem situation types (Put Together/Take Apart, Add To/Take From, Compare) do your students struggle with most, and why do you think that is?
- How might instructional shifts or visual representations help address this struggle?
- In what ways do keywords limit students’ problem-solving potential?
- How can shifting the focus to relationships between quantities improve comprehension and reasoning?
- How can applying Universal Design for Learning (UDL) principles including Multiple Means of Representation help students’ deepen their understanding of word problem structures and support diverse learners in your classroom?
References:
Achieve the Core. (n.d.). Mathematics focus by grade level. Achieve the Core. Retrieved April 5, 2025, from https://achievethecore.org/category/774/mathematics-focus-by-grade-level
Achieve the Core. (n.d.). Situation types for operations in word problems. Achieve the Core. Retrieved April 5, 2025, from https://achievethecore.org/page/932/situation-types-for-operations-in-word-problems
CAST. (2018). Universal design for learning guidelines version 2.2. CAST. Retrieved April 5, 2025, from https://udlguidelines.cast.org/
Rufo, J. M., & Martiello, R. (2024). Conquering math myths with universal design: An inclusive instructional approach for grades K–8. ASCD.

Leave a comment